The Problem

The last couple of years, I’ve been playing in a coed recreational softball league in Chicago. There are about 20 people on the team, and each week we have to decide on a batting order and fielding positions. The league has specific rules about how many men and women must be on the field at all times, and we want to make sure our friends get equal playing time.

Figuring this out manually and sharing the details was a headache, so I decided to automate and optimize the creation of our lineup and fielding assignments using linear programming. The constraints are the league rules, along with some equal playing time preferences. The objective function tries to maximize win probability.

Note: This is more of an academic exercise than anything. The optimization output is useful, but you’ll have more fun with your friends if you just show up and play!

What is Linear Programming?

Linear programming (LP) is a mathematical optimization technique that finds the best outcome in a model whose requirements are represented by linear relationships. Instead of manually trying different combinations, LP allows us to:

1. Define an objective function (what we want to maximize or minimize)
2. Add constraints (rules that must be satisfied)
3. Let the solver find the optimal solution automatically

As long as the problem can be expressed as a system of linear equations, LP can solve a wide variety of problems essentially for free. Linear programming problems are easier to document, maintain, and test than bespoke solutions.

For this softball problem, I built two separate LP models: one for fielding assignments and one for batting order.

PuLP (Software Library)

PuLP is a linear programming library for Python. It provides an interface for defining linear programming problems and delegates finding a solution to its various solvers.

Here’s the basic structure for the fielding problem:

from pulp import *

# Create the problem
problem = LpProblem("Fielding_Position_Optimization", LpMaximize)

# Decision variables: x[i][j][k] = 1 if player j plays position k in inning i
x = LpVariable.dicts("x",
    (range(num_innings), range(len(players)), range(len(Position))),
    cat=LpBinary)

# Objective: maximize skill utilization
problem += lpSum(
    players[j]["skill"] * x[i][j][k]
    for i in range(num_innings)
    for j in range(len(players))
    for k in range(len(Position))
)

# Add constraints (see below)...

# Solve using default solver
status = problem.solve()

I translated the constraints and objective function into a PuLP problem, then used the default solver to find the optimal solution. This is much simpler than a bespoke algorithm, assuming you are comfortable with a bit of linear math.

League Rules (Problem Constraints)

The league rules define the constraints of the optimization problem. The league is primarily concerned with women getting sufficient playing time.

I have added an additional constraint that ensures players (my friends) get fair playing time.

• At least four women must be on the field at all times.
• Two women must make a plate appearance every five batters.
• No player sits out two consecutive innings.

Strategy (Objective Function)

In addition to meeting the minimal problem constraints, we want to maximize “skill utilization” in our lineups. I’ve defined this as the following:

• Highly ranked players appear earlier in the lineup.
• Players only ever play positions they are comfortable with.
• Players change position as little as possible.

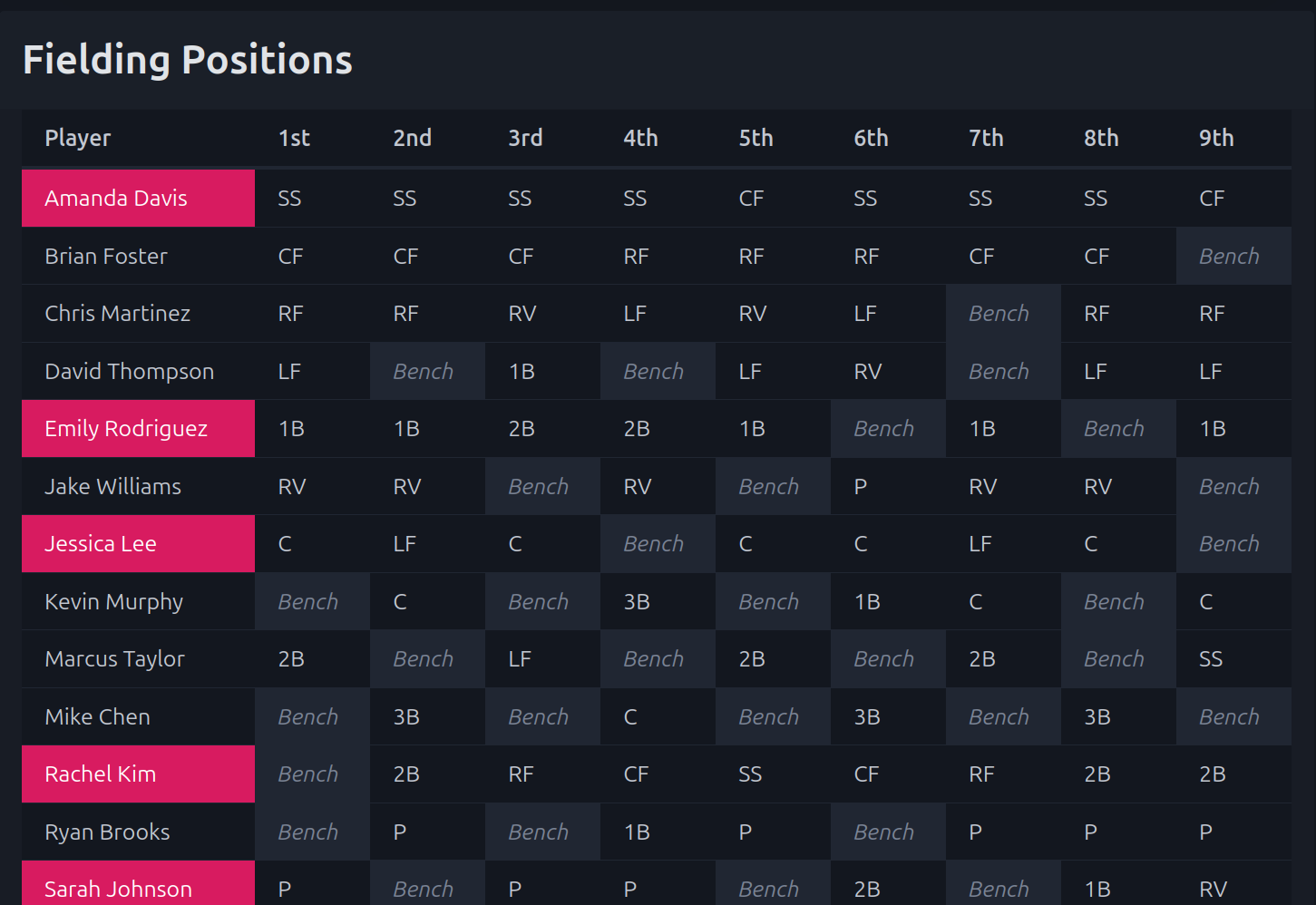
Problem 1: Fielding Assignments

The fielding problem assigns players to positions for each inning. Think of this as a 3D matrix where we need to assign:

• Players (rows in our grid)
• Positions (columns in our grid)
• Across multiple innings

Constraint: Each Position Must Be Filled

For each inning, every position must have exactly one player. The visualization below shows how we loop through each position (column) and ensure that exactly one player (somewhere in that column) is assigned:

# For each inning i, for each position k
for i in range(num_innings):
    for k in range(len(Position)):
        # Sum across all players j must equal 1
        problem += lpSum(x[i][j][k] for j in range(len(players))) == 1

Each frame represents one iteration of the inner for k loop, highlighting all player cells for that position.

Constraint: Each Player Gets At Most One Position

Similarly, each player can only be assigned to at most one position per inning. Here we loop through players (rows) and ensure no player is double-booked:

# For each inning i, for each player j
for i in range(num_innings):
    for j in range(len(players)):
        # Sum across all positions k must be <= 1
        problem += lpSum(x[i][j][k] for k in range(len(Position))) <= 1

Each frame highlights all positions for one player, showing that we’re constraining that player to have at most one assignment.

Other Fielding Constraints

Additional constraints ensure:

• At least four women on the field at all times (league rule)
• Players only play positions they are comfortable with (position preferences)
• No player sits out two consecutive innings (equal playing time)

Problem 2: Batting Order

The batting order problem is simpler—it’s a 2D assignment of players to batting positions. The same order is used throughout the game.

Constraint: Each Batting Position Has One Player

We need exactly one player at each spot in the batting order. The animation shows looping through batting positions (columns):

# For each batting position j
for j in range(num_batters):
    # Sum across all players i must equal 1
    problem += lpSum(x[i][j] for i in range(num_batters)) == 1

Constraint: Each Player Appears Exactly Once

Each player must appear exactly once in the batting order. Here we loop through players (rows):

# For each player i
for i in range(num_batters):
    # Sum across all positions j must equal 1
    problem += lpSum(x[i][j] for j in range(num_batters)) == 1

Constraint: Gender Ratio in Batting Order

One of the trickier constraints: we need at least 2 girls in every group of 5 consecutive batters (3:2 guy-to-girl ratio). The animation shows groups of 5 columns being constrained:

# For each group of 5 consecutive batters
for j in range(0, num_batters - RATIO_TOTAL, RATIO_TOTAL):
    # At least RATIO_GIRLS (2) must be female
    problem += lpSum(
        genders[i] * x[i][j + k]
        for i in range(num_batters)
        for k in range(min(RATIO_TOTAL, num_batters - j))
    ) >= RATIO_GIRLS

Results

After running both optimizations, the solver finds optimal solutions in seconds—something that would take hours to do manually, and with no guarantee of optimality.

The output provides:

• Complete fielding assignments for all innings
• Optimized batting order that maximizes team performance
• Guaranteed compliance with all league rules and fairness constraints

Why Linear Programming Matters

I strongly encourage other developers to become familiar with linear programming. It can solve a wide variety of problems essentially for free, as long as the problem can be expressed as a system of linear equations. Linear programming problems are easier to document, maintain, and test than bespoke solutions. Software Engineers should be comfortable with a table of linear equations.

Next Steps: Building the Web Application

After solving the optimization problem with PuLP, the next step was building a web application so my teammates could easily access the lineups on their phones during games. I chose a simple, server-side rendered approach:

Flask (Web Framework)

Flask is a lightweight Python web framework that makes it easy to build web applications. Since the optimization logic was already written in Python (using PuLP), Flask was a natural choice. The application flow is straightforward:

1. Users input player names, genders, and position preferences via web forms
2. Users rank players by skill level (rankings are kept private to avoid hurt feelings)
3. Flask runs the PuLP optimization on the server
4. Results are rendered and displayed in a mobile-friendly format

Pug Templating & Server-Side Rendering

Instead of building a complex single-page application (SPA), I used Pug (formerly Jade) as a templating engine. Pug provides a clean, indentation-based syntax for writing HTML templates. The key advantages:

• Server-side rendering: HTML is generated on the server and sent to the browser, so the app works without JavaScript
• Simple deployment: No build process or client-side framework complexity
• Fast initial load: Users see content immediately without waiting for JavaScript bundles to download and execute
• Mobile-friendly: Perfect for quickly checking lineups on a phone at the softball field

Here’s a simplified example of a Pug template:

extends layout

block content
  h1 Batting Order
  ol
    each player in battingOrder
      li= player.name

Pico CSS (Styling)

For styling, I used Pico CSS, a minimal CSS framework that provides beautiful defaults with almost no classes needed. It’s perfect for small projects where you want professional-looking UI without the overhead of larger frameworks.

Web Hosting & Deployment

The application is deployed as a simple Flask app, which can be hosted on platforms like:

• DigitalOcean App Platform: Easy deployment with automatic HTTPS
• Heroku: Simple git-based deployment (though pricing has changed recently)
• Railway: Modern platform with generous free tier
• Traditional VPS: Deploy with gunicorn + nginx for full control

The entire stack (PuLP + Flask + Pug + Pico CSS) is simple to maintain, costs almost nothing to host, and provides exactly what’s needed: a fast, mobile-friendly way to share optimized softball lineups with the team.

Check out the live application: softball-optimization.alexandershank.com